Teil 88
Auflösung:
Ja, die Batterien reichen für zehn Jahre, sogar für circa 11,14 Jahre!
Rechnung: Wenn die erste Batterie nach zwei Jahren erschöpft ist und die zweite eingesetzt wird, hält diese nur noch 2 x 0,9^2 = 1,62 Jahre, da sie sich bereits zwei Jahre lang um jeweils zehn Prozent entladen hat.
Wenn die zweite Batterie nach 1,62 Jahren (insgesamt 3,62 Jahren) erschöpft ist und die dritte eingesetzt wird, hält diese nur noch 2 x 0,9^3,62 = 1,37 Jahre, da sie sich bereits 3,62 Jahre lang um zehn Prozent pro Jahr entladen hat. Und so weiter...
Batterie 1: 2 Jahre
Batterie 2: 2 x 0,9^2 = 1,62 Jahre (insgesamt 3,62 Jahre)
Batterie 3: 2 x 0,9^3,62 = 1,37 Jahre (insgesamt 4,99 Jahre)
Batterie 4: 2 x 0,9^4,99 = 1,18 Jahre (insgesamt 6,17 Jahre)
Batterie 5: 2 x 0,9^6,17 = 1,04 Jahre (insgesamt 7,21 Jahre)
Batterie 6: 2 x 0,9^7,21 = 0,94 Jahre (insgesamt 8,15 Jahre)
Batterie 7: 2 x 0,9^8,15 = 0,85 Jahre (insgesamt 9 Jahre)
Batterie 8: 2 x 0,9^9 = 0,77 Jahre (insgesamt 9,77 Jahre)
Batterie 9: 2 x 0,9^9,77 = 0,71 Jahre (insgesamt 10,48 Jahre)
Batterie 10: 2 x 0,9^10,48 = 0,66 Jahre (insgesamt 11,14 Jahre)
Teil 87
Auflösung:
Ja, es geht! Die drei Freundinnen sind 26, 33 und 35 Jahre alt, also zusammen 94 Jahre!
26 = 2 x 13, 33 = 3 x 11 und 35 = 5 x 7, somit ist kein Alter eine Primzahl und je zwei sind teilerfremd!
Teil 86
Auflösung:
Es gewinnt die Spielerin, die die erste Zahl nennen darf, wenn sie mit einer eins beginnt und anschließend immer eine Zahl nennt, die zusammen mit der von der Mitspielerin genannten sieben ergibt, also zum Beispiel: 1, 3, 4, 2, 5,...
Dann lautet die Summe nach ihrer zweiten Zahl acht, nach ihrer dritten Zahl 15, dann 22, 29, 36, 43 und schließlich 50 und somit gewinnt die erste Spielerin das Spiel ohne dass die Mitspielerin es verhindern kann.
Teil 85
Auflösung:
In der Mitte einsteht durch das Herausziehen des einen Steins ein "Quadrat-Loch"!
Teil 84
Auflösung:
zwei große Dreiecke und sechs kleine
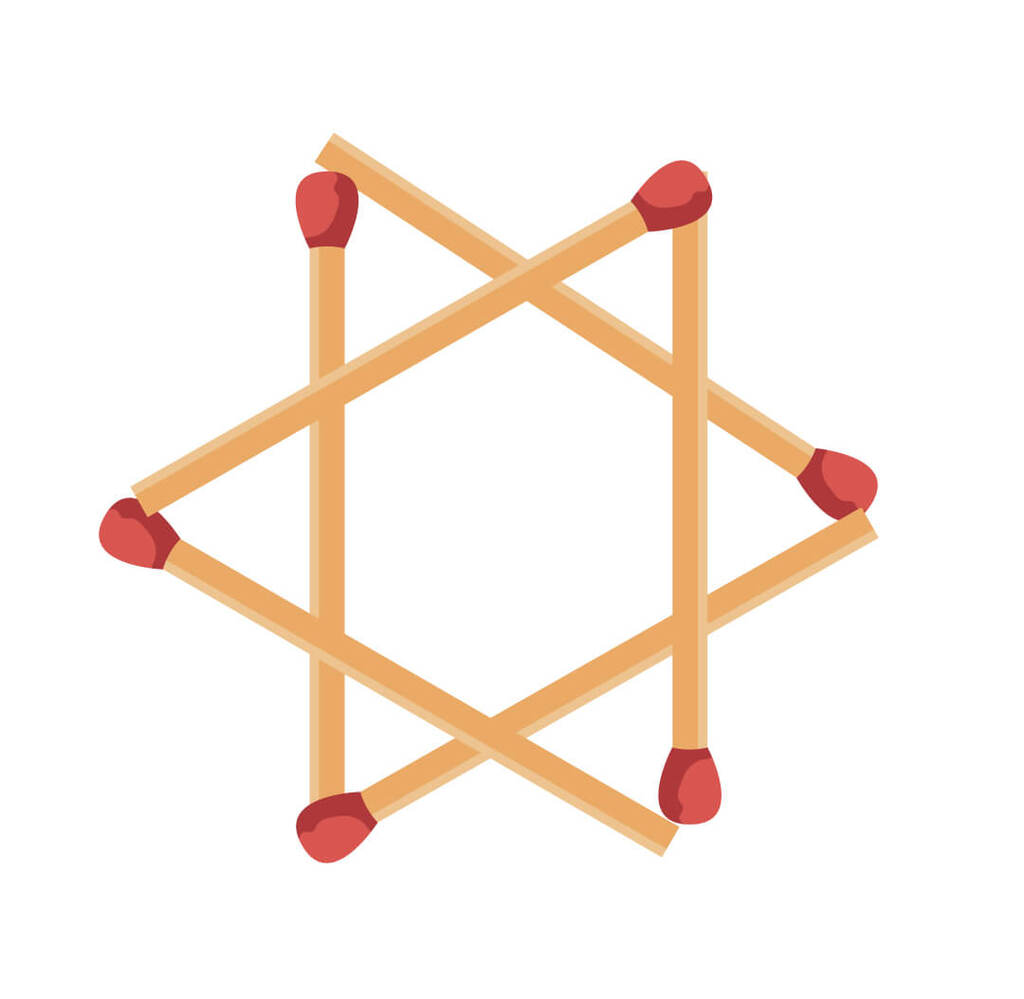
Teil 83
Auflösung:
Es gibt insgesamt 67.000 verschiedene Codes!
Für Orte mit einem Buchstaben: ein weiterer Buchstabe und eine Ziffer: 5*5*4=100
Für Orte mit einem Buchstaben: ein weiterer Buchstabe und zwei Ziffern: 5*5*4*4=400
Für Orte mit einem Buchstaben: ein weiterer Buchstabe und drei Ziffern: 5*5*4*4*4=1.600
Für Orte mit einem Buchstaben: ein weiterer Buchstabe und vier Ziffern: 5*5*4*4*4*4=6.400
Für Orte mit einem Buchstaben: zwei weitere Buchstaben und eine Ziffer: 5*5*5*4=500
Für Orte mit einem Buchstaben: zwei weitere Buchstaben und zwei Ziffern: 5*5*5*4*4=2.000
Für Orte mit einem Buchstaben: zwei weitere Buchstaben und drei Ziffern: 5*5*5*4*4*4=8.000
Für Orte mit zwei Buchstaben: ein weiterer Buchstabe und eine Ziffer: 5*5*5*4=500
Für Orte mit zwei Buchstaben: ein weiterer Buchstabe und zwei Ziffern: 5*5*5*4*4=2.000
Für Orte mit zwei Buchstaben: ein weiterer Buchstabe und drei Ziffern: 5*5*5*4*4*4=8.000
Für Orte mit zwei Buchstaben: zwei weitere Buchstaben und einer Ziffer: 5*5*5*5*4=2.500
Für Orte mit zwei Buchstaben: zwei weitere Buchstaben und zwei Ziffern: 5*5*5*5*4*4=10.000
Für Orte mit drei Buchstaben: ein weiterer Buchstabe und eine Ziffer: 5*5*5*5*4=2.500
Für Orte mit drei Buchstaben: ein weiterer Buchstabe und zwei Ziffern: 5*5*5*5*4*4=10.000
Für Orte mit drei Buchstaben: zwei weitere Buchstaben und einer Ziffer: 5*5*5*5*5*4=12.500
Teil 82
Auflösung:
Der Bau befindet sich in ca. 5,77 km Entfernung von Hühnerstall, Färberei und Rissen.
Da die drei Orte Hühnerstall, Färberei und Rissen jeweils 10 km voneinander etfernt sind,
bilden sie ein regelmäßiges/gleichseitiges Dreieck und der Bau des Osterhasen muss im Mittelpunkt des Umkreises des Dreiecks liegen, damit er von allen drei Orten gleichweit entfernt ist.
Für den Umkreis-Radius gibt es folgende Formel r = a/(2*sin alpha),
also in unserem Fall: r = 10/(2*sin60°) = 5,77 km!
Teil 81
Auflösung:
Das Wasser steht nicht einmal einen Millimeter hoch, sondern exakt 0,625 mm hoch!
5 l = 5 dm³ = 5.000 cm³ und 8 m² = 800 dm² = 80.000 cm²
Also: 5.000 cm³ / 80.000 cm² = 0,0625 cm bzw. 0,625 mm
Teil 80
Auflösung:
Das Feld ist 63,66 Meter breit!
Die beiden langen Seiten des Fußballfeldes sind zusammen schon 200 Meter lang, also müssen die beiden Halbkreise zusammen ebenfalls 200 Meter lang sein. Das heißt wir suchen einen Kreis mit dem Umfang 200 Meter. Damit ergibt sich für den Durchmesser des Kreises d = 200/π = 63,66 Meter!
Teil 79
Auflösung:
Das Feld ist 63,66 Meter breit!
Die beiden langen Seiten des Fußballfeldes sind zusammen schon 200 Meter lang, also müssen die beiden Halbkreise zusammen ebenfalls 200 Meter lang sein. Das heißt wir suchen einen Kreis mit dem Umfang 200 Meter. Damit ergibt sich für den Durchmesser des Kreises d = 200/π = 63,66 Meter!
Teil 78
Auflösung:
Das Feld ist 63,66 Meter breit!
Die beiden langen Seiten des Fußballfeldes sind zusammen schon 200 Meter lang, also müssen die beiden Halbkreise zusammen ebenfalls 200 Meter lang sein. Das heißt wir suchen einen Kreis mit dem Umfang 200 Meter. Damit ergibt sich für den Durchmesser des Kreises d = 200/π = 63,66 Meter!
Teil 77
Auflösung:
Um 15:30 Uhr stehen die beiden Zeiger im 75°-Winkel zueinander!
Der Stundenzeiger steht um 15:30 Uhr genau zwischen der drei und der vier, der Minutenzeiger genau auf der sechs. Zwischen den beiden befinden sich also "12,5 Minuten". Eine Minute entspricht 1/60 des ganzen Kreises, also 1/60 von 360° = 6°, und somit liegen zwischen den beiden Zeigern 12,5 * 6° = 75°.
Teil 76
Auflösung:
Lösung:
Partei A erhält 25 %, Partei B 20%, Partei C 28 %, Partei D 14 % und Partei E 13 %.
es gilt:
a = b + 5 = d + 6 + 5 = d + 11
b = d + 6
c = 2d
e = 13
und a + b + c + d + e = 100, also ergibt sich:
d + 11 + d + 6 + 2d + d + 13 = 100 bzw.
5d + 30 = 100
5d = 70
d = 14 und somit:
a = 25 %
b = 20 %
c = 28 %
d = 14 %
e = 13 %.
Teil 75
Auflösung:
Um 15:30 Uhr stehen die beiden Zeiger im 75°-Winkel zueinander!
Der Stundenzeiger steht um 15:30 Uhr genau zwischen der drei und der vier, der Minutenzeiger genau auf der sechs. Zwischen den beiden befinden sich also "12,5 Minuten". Eine Minute entspricht 1/60 des ganzen Kreises, also 1/60 von 360° = 6°, und somit liegen zwischen den beiden Zeigern 12,5 * 6° = 75°.
Teil 74
Auflösung:
Man ist ausreichend beleuchtet mit einer Wahrscheinlichkeit von 86,24 %.
Die Wahrscheinlichkeit, dass beide Vorderlichter ausfallen beträgt 0,1 * 0,2 = 0,02 = 2 %, also leuchtet mindestens ein Vorderlicht mit einer Wahrscheinlichkeit von 98 %.
Die Wahrscheinlichkeit, dass beide Rücklichter ausfallen beträgt 0,3 * 0,4 = 0,12 = 12 %, also leuchtet mindestens ein Rücklicht mit einer Wahrscheinlichkeit von 88 %.
Somit leuchtet mindestens ein Vorderlicht und ein Rücklicht mit
einer Wahrscheinlichkeit von 0,98 * 0,88 = 0,8624 = 86,24 %.
Teil 73
Auflösung:
Das Geschenk kann maximal die Maße
29 cm mal 19 cm mal 11 cm haben
und somit ein Volumen von 6061 cm³, also gut sechs Litern.
Teil 72
Auflösung:
3^4 * 5^2 = 81 * 25 = 2025
Teil 71
Auflösung:
Es gibt genau 88 Möglichkeiten!
Teil 70
Auflösung:
Es gibt zwei Lösungen: 3 x 51 = 153 und 6 x 21 = 126
(Ich hoffe, ich habe keine übersehen!)
Teil 69
Auflösung:
Die Masse des Originals beträgt 40 t.
Das Original ist 50 mal so lang, 50 mal so breit und 50 mal so hoch, also muss man rechnen:
50 * 50 * 50 * 320 g = 40.000.000 g = 40.000 kg = 40 t
Teil 68
Auflösung:
Die Zahl lautet 30!
Sei die gesuchte Zahl x, dann gilt: x²+2x+x+1/3x=1000 bzw. x²+10/3x-1000=0
Mit der p-q-Formel ergeben sich zwei Lösungen dieser Gleichung:
x1=-5/3-((5/3)²+1000)^1/2=-100/3 (keine natürliche Zahl)
x2=-5/3+((5/3)²+1000)^1/2=30 (gesuchte Zahl!)
Teil 67
Auflösung:
Es ist wahrscheinlicher vier Buben zu bekommen!
Skatspiel: Wenn man alle vier Buben bekommt, so erhält man also noch weitere sechs der restlichen 28 Karten. Dafür gibt es genau "28 über 6" = (28*27*26*25*24*23)/(6*5*4*3*2*1) = 376.740 Möglichkeiten. Insgesamt gibt es für die zehn Karten "32 über 10" = (32*31*30*29*28*27*26*25*24*23)/(10*9*8*7*6*5*4*63*2*1) = 64.512.240 Möglichkeiten.
Also ergibt sich eine Wahrscheinlichkeit von 376.740/64.512.240 = 0,0058 = 0,58 %
Würfel: eine von insgesamt 6*6*6 = 216 Möglichkeiten zeigt die drei Sechsen, also beträgt die Wahrscheinlichkeit 1/216 = 0,0046 = 0,46 %
Damit ist es also etwas wahrscheinlicher vier Buben zu bekommen als drei Sechsen zu würfeln.
Teil 66
Auflösung:
Als gemischter Bruch 9 9/9!
Teil 65
Auflösung:
Die dritte Zahl lautet 12!
Es gilt: (45 * 50 *x)^1/3 = 30
also: 45 * 50 * x = 30^3 = 27.000
und somit: x = 27.000 : (45 * 50) = 12
Teil 64
Auflösung:
IV x IX
IV: Römische Zahl 4
x: Malzeichen
IX: Römische Zahl 9
4 x 9 = 36
Teil 63
Auflösung:
Es gibt 114 Kombinationen, die alle drei Bedingungen erfüllen, und somit werden maximal 9 1/2 Minuten benötigt!
Es gibt fünf gerade Ziffern, also fünf Möglichkeiten für die erste Ziffer.
Da es keine Wiederholungen geben darf, gibt es für die zweite Ziffer vier, für die dritte Ziffer drei und für die vierte Ziffer noch zwei Möglichkeiten.
Insgesamt sind es also 5 * 4 * 3 * 2 = 120 Kombinationen gerader Ziffern ohne doppelte Ziffern.
Davon müssen die Datumskombinationen abgezogen werden. Hierbei gilt, dass die Ziffer 0 für ein gültiges Datum an dritter Stelle stehen muss
und somit die Ziffer zwei an erster Stelle. Die weiteren drei geraden Ziffern 4, 6 und 8 können dann beliebig an Position zwei und vier gesetzt werden.
Es ergeben sich somit 3 * 2 = 6 Datumskombinationen (2604; 2804; 2406; 2806; 2408 und 2608).
Diese müssen von den zuvor errechneten 120 Kombinationen abgezogen werden. Es verbleiben also 120 - 6 = 114 gültige Kombinationen.
Maximal werden also 114 * 5 s = 570 s = 9 1/2 min benötigt, um den Koffer zu öffnen!
Teil 62
Auflösung:
Es sind genau 24 mal!
Jedesmal, wenn die Stundenanzeige, die Minutenanzeige
und die Sekundenanzeige die gleiche Ziffenkombination anzeigen,
also um 00:00:00 Uhr,
um 01:01:01 Uhr,
um 02:02:02 Uhr,
... und zuletzt um 23:23:23 Uhr!
Teil 61
Auflösung:
Es sind genau 24 mal!
Jedesmal, wenn die Stundenanzeige, die Minutenanzeige
und die Sekundenanzeige die gleiche Ziffenkombination anzeigen,
also um 00:00:00 Uhr,
um 01:01:01 Uhr,
um 02:02:02 Uhr,
... und zuletzt um 23:23:23 Uhr!
Teil 60
Auflösung:
Die fünf treffen mit ca. 82 Prozent Wahrscheinlichkeit fünfmal!
Rechnung:
Der erste Schütze trifft mit einer Wahrscheinlichkeit von 95 %.
Der zweite Schütze trifft 24 von 25 Elfmetern, also mit einer Wahrscheinlichkeit von 96 %.
Der dritte Schütze trifft mit einer Wahrscheinlichkeit von 97 %.
Der vierte Schütze trifft 235 von 250 Elfmetern, also mit einer Wahrscheinlichkeit von 94 %.
Der fünfte Schütze trifft 198 von 200 Elfmetern, also mit einer Wahrscheinlichkeit von 99 %.
Somit ergibt sich für die Wahrscheinlichkeit, dass alle fünf Schützen treffen:
0,95 * 0,96 * 0,97 * 0,94 * 0,99 = 0,8232 = 82 %
Teil 59
Auflösung:
Im Normalpreis kostet die günstigste Flasche € 7,10, die mittlere Flasche € 10,49 und die teuerste Flasche € 13,99.
Rechnung: € 24 : 76% = € 31,58 (Normalpreis)
x-3,39 + x + x+3,50 = 31,58 bzw. 3x + 0,11 = 31,58 bzw. 3x = 31,47 bzw. x = 10,49
Also kostet die günstigste Flasche € 10,49 - € 3,39 = € 7,10, die
mittlere Flasche € 10,49 und die teuerste Flasche € 10,49 + € 3,50 = € 13,99!
Teil 58
Auflösung:
Unter der Voraussetzung, dass alle 24 teilnehmenden Mannschaften gleich stark spielen, hat natürlich jede der 24 Mannschaften die gleiche Chance auf den Titel und somit hat jede Mannschaft, also auch die deutsche, die gleiche Titelchance, nämlich 1/24.
Teil 57
Auflösung:
3/44 bzw. ca. 6,8%
Die Wahrscheinlichkeit für drei weiße beträgt: 5/12 * 4/11 * 3/10 = 60/1320
Die Wahrscheinlichkeit für drei gelbe beträgt: 4/12 * 3/11 * 2/10 = 24/1320
Die Wahrscheinlichkeit für drei weiße beträgt: 3/12 * 2/11 * 1/10 = 6/1320
insgesamt: 60/1320 + 24/1320 + 6/1320 = 90/1320 = 3/44 = 6,8%
Teil 56
Auflösung:
Satt für 24 Tage wird der Vorrat nur für 21 Tage reichen!
8 * 24 = 192 Es sind 192 Tagesrationen vorhanden.
8 * 15 = 120 Nach 15 Tagen sind 120 Tagesrationen verbraucht.
192 - 120 = 72 Es sind nach 15 Tagen noch 72 Tagesrationen übrig.
72 / 12 = 6 Die 72 Tagesrationen reichen noch für sechs weitere Tage.
15 + 6 = 21 Der Vorrat reicht für insgesamt 21 Tage.
Teil 55
Auflösung:
(2 + 2 + 2 + 2) * (2 + (2 + 2 + 2 + 2) : 2 + 2 : 2) - 2
= 8 * (2 + 8 : 2 + 1) - 2
= 8 * (2 + 4 + 1) - 2
= 8 * 7 -2
= 56 - 2
= 54
Teil 54
Auflösung:
Die gesamte Streckenlänge beträgt 8400 m!
Die Laufstrecke bildet ein rechtwinkliges Dreieck und somit lässt sich mit dem Satz des Pythagoras die dritte Seite ausrechnen: a²+b²=c², also c²=2100²+2800², bzw. c²=12250000 und somit c=3500 m und die gesamte Laufstrecke: 2100 m + 2800 m + 3500 m = 8400 m
Teil 53
Auflösung:
Die Eier reichen für maximal 16 Nester!
(0/0/1), (0/1/0), (1/0/0), (0/1/1),
(1/0/1), (1/1/0), (0/0/2), (0/2/0),
(2/0/0), (0/1/2), (0/2/1), (1/0/2),
(1/2/0), (2/0/1), (2/1/0), (1/1/1)
Teil 52
Auflösung:
Die Augensumme beträgt 1393!
Die gegenüberliegenden Seiten eines Würfels haben immer die Augensumme 7.
Da von jedem der 99 Würfel jeweils zweimal zwei gegenüberliegende Seiten zu sehen sind, sind es pro Würfel 14 Augen.
Zusätzlich hat der erste und der letzte Würfel noch eine offene Seite, deren Augen zusammen ebenfalls 7 ergeben müssen.
Somit ergeben sich 99 * 14 + 7 = 1393 Augen!
Teil 51
Auflösung:
Es gibt 48 verschiedene Möglichkeiten!
Franz kann sich einen beliebigen Platz aussuchen, aber da es ein runder Tisch ist, macht es keinen Unterschied, welchen der sechs Plätze er einnimmt. Hans hat dann zwei Möglichkeiten sich neben ihm zu platzieren, für den dritten Freund gibt es dann noch vier freie Plätze, für den vierten drei, für den fünften zwei und für den letzten nur noch einen, also 1*2*4*3*2*1=48 Möglichkeiten!
Teil 50
Auflösung:
Es sind € 967,82!
Für diesen Betrag erhielte man in einem ganzen Jahr € 36,78 Zinsen. Anteilig für 22 Tage im Februar, neun ganze Monate à 30 Tage und 23 Tage im Dezember, also für 315 von 360 Banktagen eines Jahres € 32,18 Zinsen.
Teil 49
Auflösung:
der Milchreis (um 63,21 %)
Rechnung:
Milchreis: 1000/800 * 2,99/2,29 = 1,6321 => 63,21 % teurer
Stieleis: 4/3 * 110/90 = 1,6296 => 62,96 % teurer
Teil 48
Auflösung: 33
24.11.2001
14.12.2001
14.11.2002
12.11.2004
21.11.2004
11.12.2004
24.11.2010
14.12.2010
24.01.2011
14.02.2011
12.04.2011
21.04.2011
24.10.2011
04.12.2011
14.01.2012
11.04.2012
14.10.2012
04.11.2012
12.01.2014
21.01.2014
11.02.2014
12.10.2014
21.10.2014
02.11.2014
20.11.2014
01.12.2014
10.12.2014
14.11.2020
14.01.2021
11.04.2021
14.10.2021
04.11.2021
Teil 47
Auflösung:
Befana, Christkind, Nikolaus, Ruprecht, Weihnachtsmann
Rechnung:
Da Befana ganz links wohnt und Ruprecht rechts vom Nikolaus, gibt es lediglich sechs Möglichkeiten, die man überprüfen kann:
Befana, Nikolaus, Ruprecht, Weihnachtsmann, Christkind (falsch, Christkind hat nur einen Nachbarn)
Befana, Nikolaus, Ruprecht, Christkind, Weihnachtsmann (falsch, Nikolaus und Weihnachtsmann haben keinen gemeinsamen Nachbarn)
Befana, Weihnachtsmann, Christkind, Nikolaus, Ruprecht (falsch, Weihnachtsmann und Weihnachtshexe wohnen nebeneinander)
Befana, Christkind, Weihnachtsmann, Nikolaus, Ruprecht (falsch, Nikolaus und Weihnachtsmann haben keinen gemeinsamen Nachbarn)
Befana, Weihnachtsmann, Nikolaus, Ruprecht, Christkind (falsch, Weihnachtsmann und Weihnachtshexe wohnen nebeneinander)
Befana, Christkind, Nikolaus, Ruprecht, Weihnachtsmann (richtig, alle Bedingungen sind erfüllt!)
Teil 46
Auflösung:
Athos sechs, Porthos elf und Aramis fünfzehn, zusammen 32!
Rechnung:
Athos hat x Duelle bestritten
Porthos hat dementsprechend x+5 Duelle bestritten
Aramis hat folglich x+x+5-2 = 2x+3 Duelle bestritten
zusammen haben sie also x+x+5+2x+3 = 4x+8 Duelle bestritten
also gilt:
30 <= 4x+8 <= 35 | -8
22 <= 4x <= 27 | :4
5,5 <= x <= 6,75
also muss x = 6 gelten, da x ja eine ganze Zahl sein muss!
also Athos x = 6 Duelle, Porthos x+5 = 6+5 = 11 Duelle und Aramis 2x+3 = 2*6+3 = 15 Duelle, zusammen 32 Duelle!
Teil 45
Auflösung:
Es sind acht! 13, 17, 31, 37, 71, 73, 79, 97
Teil 44
Auflösung:
nach 80 Minuten! Dann befinden sich in beiden Eimern jeweils 4,8 Liter
zehn Liter = 10.000 ml
6,5 cl = 65 ml
im ersten Eimer befinden sich somit nach t min: 10.000 - 65 * t ml
im zweiten Eimer befinden sich nach t min: 65 * t - 5 * t ml
für Gleichheit muss also gelten:
10.000 - 65 * t = 65 * t - 5 * t, also 10.000 = 125 * t bzw. t = 80 min
erster Eimer: 10.000 - 65 * 80 = 4.800 ml = 4,8 l
zweiter Eimer: 65 * 80 - 5 * 80 = 4800 ml = 4,8 l
Teil 43
Auflösung:
Das Fußballfeld ist ca. 63,66 m breit!
Die Bogenlänge eines Halbkreises muss 100 m lang sein, also der Umfang eines entsprechenden Kreises 200 m, damit die Stadionrunde 400 m lang ist.
Die gesuchte Breite b des Feldes ist gleichzeitig der Durchmesser des Kreises.
also gilt pi * b = 200 bzw. b = 200/pi = 63,66!
Teil 42
Auflösung:
Sie wird 1,50 m hoch! 1.400 kg Marmor haben ein Volumen von 0,5 m³
und somit reicht es für eine Pyramide mit 1 m² Grundfläche
und 1,50 m Höhe: V = 1/3 * 1 m² * 1,5 m = 0,5 m³
Teil 42
Auflösung:
Sie wird 1,50 m hoch! 1.400 kg Marmor haben ein Volumen von 0,5 m³
und somit reicht es für eine Pyramide mit 1 m² Grundfläche
und 1,50 m Höhe: V = 1/3 * 1 m² * 1,5 m = 0,5 m³
Teil 39
Auflösung:
Die Länge des Rands beträgt fast 128 Meter!
Teil 38
Auflösung:
Es sind 25!
(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97)
Teil 37
Auflösung:
Wir müssten mit 280 km/h fahren!
erster Streckenabschnitt: 2:18 h und 130 km/h ==> 2,3 h * 130 km/h = 299 km
zweiter Streckenabschnitt: 0:30 h und 5 km
für den dritten Streckenabschnitt verbleiben also 0:12 h für 56 km ==> 56 km / 0,2 h = 280 km/h
Teil 36
Auflösung:
Es gibt 5.544.000 verschiedene Kombinationen!
Elf verschiedene Elemente lassen sich auf 11! = 11*10*9*8*7*6*5*4*3*2*1 = 39.916.800 verschiedene Arten anordnen. Da aber E und R jeweils dreifach vorkommen und das S doppelt, muss diese Zahl zweimal durch 3! = 3*2*1 = 6 und einmal durch 2! = 2*1 = 2 geteilt werden, da das Vertauschen von drei gleichen Buchstaben auf sechs Arten und das vertauschen von zwei gleichen Buchstaben auf zwei Arten geht, ohne dass ein neues Wort entsteht. Somit also: 39.916.800:6:6:2 = 39.916.800:72 = 554.400 Um aus diesen elf angeordneten Buchstaben aber zwei Worte zu machen, gibt es immer genau zehn Möglichkeiten, die Lücke zwischen zwei Buchstaben zu setzen und so zwei Worte entstehn zu lassen. Somit kommt man auf 10 * 554.400 = 5.544.000 Möglichkeiten!
Die kurze Rechnung sieht also so aus: 10 * 11! / (3! * 3! * 2!) = 5.544.000
Teil 35
Auflösung:
Es gibt 5.040 verschiedene Worte/Kombinationen!
Acht verschiedene Elemente lassen sich auf 8! = 8*7*6*5*4*3*2*1 = 40.320 verschiedene Arten anordnen.
Da aber drei Buchstaben (E, R und S) doppelt vorkommen, muss diese Zahl dreimal durch zwei geteilt werden,
da das Vertauschen von zwei E (oder R oder S) miteinander ja kein neues Wort generiert.
Somit also: 40.320:2:2:2 = 40.320:8 = 5.040
Teil 34
Auflösung:
Es sind noch 72 Minuten!
Rechnung: 120 min / LSF 50 + 120 min / LSF 30 + x min / LSF 20 = 10 min ergibt:
x = (10 - 120/50 + 120/30) * 20 = 72 min
Teil 33
Auflösung:
Es sind knapp 50 Liter Luft in der Blase!
(Der Durchmesser der Seifenblase beträgt etwa 45,64 cm.)
Teil 32
Auflösung:
Man muss bei Kind neun anfangen!
Teil 31
Auflösung:
--> zu Beginn befinden sich also im acht- Liter-Eimer acht Liter,
im fünf-Liter-Eimer null Liter, ebenso im drei-Liter-Eimer: (8/0/0)
--> der fünf-Liter-Eimer wird mit dem acht-Liter-Eimer gefüllt: (3/5/0)
--> der drei-Liter-Eimer wird mit dem fünf-Liter-Eimer gefüllt: (3/2/3)
--> der drei-Liter-Eimer wird in den acht-Liter-Eimer entleert: (6/2/0)
--> der fünf-Liter-Eimer wird in den drei-Liter-Eimer entleert: (6/0/2)
--> der fünf-Liter Eimer wird mit dem acht-Liter-Eimer gefüllt: (1/5/2)
--> der drei-Liter-Eimer wird mit dem fünf-Liter-Eimer gefüllt: (1/4/3)
--> der drei-Liter-Eimer wird in den acht-Liter-Eimer entleert: (4/4/0)
Somit erhält man zweimal vier Liter!
Teil 30
Auflösung:
D1+2+3+4+5+8+9+10=42
6*7=42
Teil 29
Auflösung:
Der Mittelpunkt lautet M(1/2) und der Radius r = 5 Längeneinheiten.
Teil 28
Auflösung
Leicht:
47 | 52 | 51 |
54 | 50 | 46 |
49 | 48 | 53 |
Mittel:
31 | 42 | 41 | 36 |
40 | 37 | 30 | 43 |
34 | 39 | 44 | 33 |
45 | 32 | 35 | 38 |
Schwer:
20 | 37 | 24 | 41 | 28 |
33 | 25 | 42 | 29 | 21 |
26 | 38 | 30 | 22 | 34 |
39 | 31 | 18 | 35 | 27 |
32 | 19 | 36 | 23 | 40 |
Teil 27
Auflösung
Man macht es mit den Römischen Zahlen:
12 = XII
Wenn man die Zahl waagerecht in der Mitte teilt, so lautet der obere Teil VII = 7!
Teil 26
Auflösung
X=0, da eine Zahl durch elf teilbar ist, wenn die Differenz aus der Summe der Ziffern an den ungeraden Stellen (1+3+5+7+9+0+8+6+4+2+X=45+X) und der Summe der Ziffern an den geraden Stellen (2+4+6+8+0+9+7+5+3+1=45) selber eine durch elf teilbare Zahl ergibt.
Teil 25
Auflösung
Es ist egal, für jeden der fünf besteht die gleiche Wahrscheinlichkeit, das kürzere Stäbchen zu ziehen, unabhängig davon, ob er als erster, zweiter, dritter, vierter oder eben als letzter zieht!
(Andernfalls wäre das Ziehen ja auch als Zufallsentscheidung ungeeignet!)
Teil 24
Auflösung
17. 06. 2345
Teil 23
Auflösung
Im Achter-System (oder auch Oktalsystem)
entspricht der Rechnung 668 × 668 = 446224 im Zehner-System
(bzw. Dezimal-System)
Teil 22
Auflösung
Für beliebigen Durchmesser d gilt:
Das Volumen einer Kugel ist proportional zu d³, also ist das Volumen der großen Kugel achtmal so groß wie das Volumen der kleinen Kugel: Ruprecht benötigt acht kleine Kugeln für eine große Kugel!
Die Oberfläche einer Kugel ist proportional zu d², also ist die Oberfläche der großen Kugel viermal so groß wie die Oberfläche der kleinen Kugel: Ruprecht benötigt die Goldfolien von vier kleinen Kugeln für eine große Goldfolie.
Der Umfang einer Kugel ist proportional zu d, also ist der Umfang der großen Kugel doppelt so groß wie der Umfang der kleinen Kugel: Ruprecht benötigt die Bändchen von zwei kleinen Kugeln für ein großes Bändchen.
Teil 21
Auflösung
A schafft es pro Stunde 1/48 der Garage leerzupumpen, B entsprechend 1/96 und C 1/192.
Somit muss die Gleichung 1/48 * t + 1/96 * t + 1/192 * t = 1 gelöst werden.
Es ergibt sich: t ist ungefähr 27,43 h bzw. 27 h 25 min 42,86 s
Also nach knapp 27 1/2 h ist die Garage leergepumpt.
Teil 20
Auflösung
Er befindet sich noch 39,90 m vor dem Ziel.
Quentin fährt 3980 m in der gleichen Zeit, in der Paul 4000 m fährt, also ist seine
Geschwindigkeit 3980/4000 = 199/200 der Geschwindigkeit Pauls. Gleiches gilt für Oskar im
Verhältnis zu Quentin. Somit ist Oskars Geschwindigkeit 199/200 * 199/200 = 39601/40000 der Geschwindigkeit Pauls
und somit schafft er 3960,10 m während Paul 4000 m fährt und befindet sich 39,90 m vor dem Ziel.
Teil 19
Auflösung
28! Die Teiler lauten: 1, 2, 4, 7, 14 und 28 und die Summe -ohne
die 28 selbst- lautet: 1 + 2 + 4 + 7 + 14 = 28!
(Die nächste ist übrigens erst die 496!)
Teil 18
Auflösung
Die Länge des direkten Wegs beträgt 20 m, sie lässt sich mit einem rechtwinkligen Dreieck und dem Satz des Pythagoras berechnen!
Die Katheten haben die Längen (48 m - 36 m =) 12 m und 16 m, somit hat die gesuchte Hypotenuse die Länge (((12 m)² + (16 m)²)^½ =) 20 m!
Teil 17
Auflösung
Es waren genau 18 Münzen.
Neun erhält die älteste Enkelin, sechs die mittlere und drei die jüngste.
Teil 16
Auflösung
Es gibt genau sechs verschiedene Möglichkeiten die drei Briefe in die drei Briefkästen zu werfen, die alle gleichwahrscheinlich sind, da Klaus ja zufällig handelt. Dabei ist in einem Fall alles richtig, in drei Fällen ist genau ein Brief im richtigen Kasten und in zwei Fällen keiner. (Es gibt keine Möglichkeit für genau zwei richtig verteilte Briefe!)
Also ergeben sich folgende Wahrscheinlichkeiten:
P(3 richtig) = 1/6 = 16,7 %
P(2 richtig) = 0/6 = 0 %
P(1 richtig) = 3/6 = 1/2 = 50 %
P(0 richtig) = 2/6 = 1/3 = 33,3 %
Teil 15
Auflösung
Die zehnte Zahl lautet 121!
Die erste Zahl wird nämlich durch vier geteilt (8:4=2), anschließend wird zwei addiert (2+2=4) und als drittes wird die Zahl quadriert(4²=16). Danach beginnt es wieder von vorn mit dem Teilen durch vier, und so muss am Ende die 11 erneut quadriert werden und so ergibt sich die heutige Lösung 121.
Teil 14
Auflösung
Neun Münzen (1 Cent, 2 * 2 Cent, 5 Cent, 2 * 10 Cent, 20 Cent, 50 Cent und 1 Euro)
Teil 13
Auflösung
Da es innerhalb von 12 Stunden elfmal geschieht, dauert es 12/11 Stunden, das sind ungefähr eine Stunde fünf Minuten und 27 Sekunden.
Teil 12
Auflösung
Nein, Ingo kann es nicht!
Wenn man das gesamte Spielfeld mit einem Schachbrettmuster überzieht, so fehlen an den beiden Ecken entweder zwei weiße oder zwei schwarze Quadrate, das heißt, entweder bleiben 30 weiße und 32 schwarze Felder übrig oder umgekehrt. Da man aber mit jedem Dominostein immer genau ein weißes und genau ein schwarzes Feld abdeckt, bleiben für den letzten Dominostein entweder zwei schwarze oder zwei weiße Felder übrig, die nicht nebeneinander liegen können und daher auch nicht mit einem Stein abgedeckt werden können.
Teil 11
Auflösung
Es sind 23 Personen!
Bei den folgenden Berechnungen lassen wir den 29. Februar unberücksichtigt.
(Aber es gilt auch, wenn man ihn berücksichtigt.)
Bei zwei Personen beträgt die Wahrscheinlichkeit, dass sie an verschiedenen Tagen Geburtstag haben: 365/365 * 364/365 = 0,9973 = 99,73 %,
also die Wahrscheinlichkeit, dass zwei (die beiden) Personen am gleichen Tag Geburtstag haben: 1 - 365/365 * 364/365 = 1 - 0,9973 = 0,27 %.
drei Personen: verschiedene Geburtstage: 365/365 * 364/365 * 363/365 = 0,9918 = 99,18 %, zwei am gleichen Tag Geburtstag also: 1 - 0,9918 = 0,82 % u.s.w.
n Personen: verschiedene Geburtstage: (365 * 364 * ... * (365-n+1))/365^n = 365!/((365-n)! * 365^n), zwei am gleichen Tag: 1 - 365!/((365-n)! * 365^n)
für n=22 erhält man 47,57 %, für n=23 erhält man 50,73 %!
Teil 10
Auflösung
Es sind 45 Erdbeeren!
Fritz isst ein Drittel der Erdbeeren und Gabi von den restlichen zwei Dritteln 40 %, d.h. 2/3 * 40 % = 2/3 * 40/100 = 4/15,
also isst Fritz von den Erdbeeren 1/3 - 4/15 = 1/15 mehr als Gabi und dies entspricht drei Erdbeeren,
also muss die Gesamtzahl der Erdbeeren die fünzehnfache Menge sein, also sind es 45 Erdbeeren!
Teil 9
Auflösung
Lösung: Elena reichen drei Versuche!
Im Folgenden steht E für eine beliebige bereits als echt erkannte Münze.
1. Wiegen: Münzen 1,2,3,4 versus Münzen 5,6,7,8
Fall A: Die Münzen sind gleich schwer, also sind die Münzen 1, 2, 3, 4, 5, 6, 7 und 8 echt.
2. Wiegen: Münzen 9,10,11 versus Münzen E,E,E
Möglichkeit 1: Die Münzen sind gleich schwer, also auch 9, 10 und 11 sind echt und Münze 12 muss falsch sein.
3. Wiegen: Münze 12 versus Münze E
(--> Die Münzen sind gleich schwer, ist nicht möglich!)
--> Münze 12 ist leichter, also ist sie die leichtere falsche Münze.
--> Münze 12 ist schwerer, also ist sie die schwerere falsche Münze.
Möglichkeit 2: 9, 10, 11 sind leichter, also ist eine davon die leichtere falsche Münze und Münze 12 ist echt.
3. Wiegen: Münze 9 versus Münze 10
--> Die Münzen sind gleich schwer, also sind sie beide echt und Münze 11 ist die leichtere falsche Münze.
--> Münze 9 ist leichter, also ist sie die leichtere falsche Münze.
--> Münze 10 ist leichter, also ist sie die leichtere falsche Münze.
Möglichkeit 3: 9, 10, 11 sind schwerer, also ist eine davon die schwerere falsche Münze und Münze 12 ist echt.
3. Wiegen: Münze 9 versus Münze 10
--> Die Münzen sind gleich schwer, also sind sie beide echt und Münze 11 ist die schwerere falsche Münze.
--> Münze 9 ist schwerer, also ist sie die schwerere falsche Münze.
--> Münze 10 ist schwerer, also ist sie die schwerere falsche Münze.
Fall B: Die Münzen 1, 2, 3, 4 sind leichter, also sind die Münzen 9, 10, 11 und 12 echt und entweder eine der
Münzen 1, 2, 3 oder 4 die leichtere falsche oder eine der Münzen 5, 6, 7 oder 8 die schwerere falsche.
2. Wiegen: Münzen 1,2,5 versus Münzen 3,6,E
Möglichkeit 1: Die Münzen sind gleich schwer, also sind auch die Münzen 1, 2, 3, 5 und 6 echte Münzen und
entweder 4 die leichtere falsche Münze oder eine der beiden Münzen 7 und 8 die schwerere falsche Münze.
3. Wiegen: Münze 7 versus Münze 8
--> Die Münzen sind gleich schwer, also sind sie beide echt und Münze 4 ist die leichtere falsche Münze.
--> Münze 7 ist schwerer, also ist sie die schwerere falsche Münze.
--> Münze 8 ist schwerer, also ist sie die schwerere falsche Münze.
Möglichkeit 2: Die Münzen 1, 2 und 5 sind leichter, also sind die Münzen 4, 7 und 8 echte Münzen und
entweder 6 die schwerere falsche Münze oder eine der beiden Münzen 1 und 2 die leichtere falsche Münze.
3. Wiegen: Münze 1 versus Münze 2
--> Die Münzen sind gleich schwer, also sind sie beide echt und Münze 6 ist die schwerere falsche Münze.
--> Münze 1 ist leichter, also ist sie die leichtere falsche Münze.
--> Münze 2 ist leichter, also ist sie die leichtere falsche Münze.
Möglichkeit 3: Die Münzen 1, 2 und 5 sind schwerer, also sind die Münzen 4, 7 und 8 echte Münzen und
entweder ist die Münze 5 die schwerere falsche Münze oder Münze 3 die leichtere falsche Münze.
3. Wiegen: Münze 3 versus Münze E
--> Die Münzen sind gleich schwer, also ist Münze 3 echt und Münze 5 ist die schwerere falsche Münze.
--> Münze 3 ist leichter, also ist sie die leichtere falsche Münze.
(--> Münze 3 ist schwerer, ist unmöglich)
Fall C: Die Münzen 1,2,3,4 sind schwerer, also sind die Münzen 9, 10, 11 und 12 echt und entweder eine der Münzen 1, 2, 3 oder 4 die schwerere falsche oder eine der Münzen 5, 6, 7 oder 8 die leichtere falsche.
Dieser Fall ist spiegelverkehrt zu Fall B. (Man vertausche einfach die Nummern 1, 2, 3 und 4 mit 5, 6, 7 und 8.)
Somit erkennt Elena in jedem Fall nach dem dritten Wiegen welche Münze nicht echt ist und ebenfalls ob sie zu leicht oder zu schwer ist.
Teil 8
Auflösung
Für x, y und z kommen ja nur einstellige Primzahlen (2, 3, 5 und 7) infrage,
also kommen als zweistellige Primzahlen xy und yz auch
nur Kombinationen aus diesen vier Ziffern in Betracht: 23, 37, 53 und 73.
Somit kommen für xyz wiederum also nur die vier folgenden Kombinationen infrage:
237, 373, 537 und 737. Von diesen vier Zahlen ist aber lediglich 373 eine
Primzahl und somit die Lösung dieses Rätsels!
Teil 7
Auflösung
Ja, es ist möglich!
Teil 6
Auflösung
Ja, es ist möglich!
Teil 5
Auflösung
Ja, Donald passt problemlos unter dem Seil durch!
Rechnen wir mit dem Erdradius 6.371 km den Umfang aus, so ergibt sich eine Länge
von 40.030,17359 km. Mit dem um einen Meter auf 40.030,17459 erhöhten
Umfang ergibt sich der neue Radius 6.371,000159 km. Also schwebt das Seil 15,9 cm über
dem Boden und das reicht locker für den dicken Donald aus!
Das interessante (und unerwartete) an der Aufgabe ist, dass dieser Abstand proportional
zur Seilverlängerung ist und unabhängig vom Radius der Kugel!
Das bedeutet einerseits, dass bei einer Verlängerung des Seils um zwei Meter das Seil um
31,8 cm über dem Boden schweben würde und andererseits, dass bei jeder Kugel (oder Kreis) ein Seil,
das ein Meter länger als der Umfang der Kugel (des Kreises) ist,
der Abstand zur Kugel (zum Kreis) immer 15,9 cm beträgt!
Teil 4
Auflösung
Clara zahlt weniger! Genauer gesagt, sie spart 0,25 % des ursprünglichen Verkaufspreises.
Der ursprüngliche Preis entspricht 100 % (z. B. € 2.000), nach der Erhöhung um
fünf Prozent sind es also 105 % des ursprünglichen Preises (im Beispiel also € 2.100)
Hiervon werden nun wiederum fünf Prozent abgezogen 5 % von 105 % des ursprünglichen Preises sind
5,25 % des ursprünglichen Preises (im Beispiel also € 105). Zieht man nun diese
5,25 % von den 105 % ab so bleiben 99,75 % des ursprünglichen Preises übrig (im Beispiel € 1.995).
Also zahlt Clara letztlich 0,25 % des ursprünglichen Preises weniger (im Beispiel spart sie fünf Euro).
Teil 3
Auflösung
In jedem Fall (egal wie groß die Gläser und Löffel sind) ist es hinterher gleichviel,
denn die Menge rote Flüssigkeit, die im ersten Glas fehlt und sich im zweiten Glas befindet,
wird durch die gleiche Menge farbloser Flüssigkeit ersetzt, die jetzt wiederum im zweiten Glas fehlt.
Teil 2
Auflösung
x: Preis eines Weltmeister-Brötchens
y: Preis eines Sonnenblumenkern-Brötchens
Aufstellen eines Linearen Gleichungssystems:
I: 7 x + 8 y = 11,15 |* 9
II: 11 x + 9 y = 14,70 |* 8
I: 63 x + 72 y = 100,35
II: 88 x + 72 y = 117,60
II-I: 25 x = 17,25 | : 25
X = 0,69 d.h. ein Weltmeister-Brötchen kostet € 0,69
X in I: 7 * 0,69 + 8 y = 11,15
4,83 + 8 y = 11,15 | - 4,83
8 y = 6,32 | : 8
Y = 0,79 d.h. ein Sonnenblumenkern-Brötchen kostet € 0,79
10 * € 0,69 + 12 * € 0,79 = € 16,38
Anna muss kommenden Sonntag € 16,38 bezahlen!
Teil 1
Auflösung
Es gibt 2 Möglichkeiten:
A= 3, B=2, C=5, D=8, E=4, F=1, G=0 und H=6
oder
A= 8, B=2, C=4, D=3, E=5, F=1, G=9 und H=6
Einen klar strukturierten Ansatz gibt es nicht. Hier muss man logisch vorgehen.
Man sieht auf den ersten Blick, dass F=1 sein muss, da man zwei vierstellige Zahlen addiert und das Ergebnis fünfstellig ist.
H muss als Summe zwei gleicher Zahlen eine gerade Zahl sein.
C und E müssen zwei aufeinanderfolgende Zahlen sein. Und dann muss man ein wenig ausprobieren.
